Black Fridays

GEK1517 Tutorial One: Consider the problem: Is there at least one Black Friday (Firday the thirteenth) in every year? How would you approach such a problem?

a. Of course, being a kid spoilt with the power of computers, the first thing I thought of was of course to devise a computer algorithm which will sift through the calendars of past, present and future years until it arrives at a Black-Friday-less year.

If there is one year where Black Friday does not exist, of course this will be fine. But if there isn't one, this method can never prove that every year must feature a Black Friday. "So you have tested a lot of cases! But have you tested all cases? No! What if the next year has no Black Friday? and so on ad infinitium.)

b. A better way would be to simplify the problem into patterns.
So I temporary f-ked the maths and went into empirical observation. From my handphone calendar, I observed that the 13th days in the months of January, February, etc. fell in this pattern:

{Wed Sat Sat Tue Thu Sun Tue Fri Mon Wed Sat Mon}

How to make sense of this pattern?
Recall that in non-leap years, the number of days in every month are the same.
So, as an example, January is always 31 days long.
It follows that 1 Feb is always 31 days after 1 Jan.
After which we can see that 13 Feb is always 31 days after 13 Jan.

However, you want to express this rule in days of the week (d.o.w.). So 31 days after Wednesday will be a Saturday, because

31 days = 4 times (7 days) + 3 days

Apply this to the pattern above and you can see that only the last term (+3 days) is needed: 13 Jan 2010 lies on a Wednesday, 28 days is exactly four weeks, so 28 days after 13 Jan is still on a Monday. We are only concerned with how the day of the week change, so the former term can boot it. And we write:

January -> February: 3 days
(to obtain the d.o.w for 13 Feb from 13 Jan, we skip forward 3 days in the week)

By this line of thought, Sunday + 1 is Monday.
So it makes sense to visualise the cycle of the week using a number line which looks like this:

Meanwhile, we obtain from the year 2010:
February -> March: 0 days
March -> April: 3 days
etc.
and we arrive at this twelve skip-forward values, from Jan->Feb to Dec->Jan

{3, 0, 3, 2, 3, 2, 3, 2, 3, 3, 2, 3, 2}

Be reminded that since number of days every January/February/etc. for different non-leap years are the same, these skip-forward values apply to all non-leap years.
How to make a conclusion from this array?
We take out the number line again, and put the month on the d.o.w its 13th day lands on, using the twelve skip-forward values for each month after January.
Anyway,

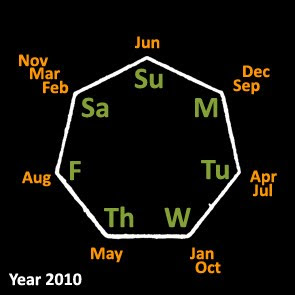All the days of the week are covered!
You'd be glad (or infuriated) that this says the same thing as the array

{Wed Sat Sat Tue Thu Sun Tue Fri Mon Wed Sat Mon}

But now it is clear that that it makes it obvious that no matter what day 13 Jan lies on in some other year, there will be a black friday somewhere down the year:

To solve for leap years, just take note that a leap-year February has one more day than a non-leap-year February. So the skip-forward value for February->March in a leap year is 1. The other values stay the same.

We see that even in a leap year, the 13th days of the month cover all days of the week. (What I did to introduce the gap of 1 between February and March was just to shift February and January one step earlier)


Yep, the leap year also covers all the days of the week.

[Spoiler: lecturer presented a one-size-fit-all-years solution which ignores February.]

To arrive at the lecturer's strong case, the only step we need to make is to shave of the superfluous months that crowd uselessly at a d.o.w.


The consecutive months of December to April are discounted, and since February is left out of consideration, the same diagram can demonstrate both leap and non-leap years.

-END OF DEMONSTRATION-