Bishop George Berkeley

"Men learn the elements of science from others;
and every learner hath a deference more or less to authority,
especially the younger learners,
few of that kind caring to dwell long upon principles,
but including rather to take them on trust:
And things early admitted by repetition become familiar:
And this familiarity at length passeth for evidence."

-- A Defence of Freethinking in Mathematics (1735)

The Chemistry of Plant Communications

Somehow, plants show up very frequently in my first semester. First lallang for WP2201I, now plant pheromones for CM1417. I can't put a finger on what is really going on despite having chosen the topics myself.

Picture taken from:
Takabayashi, J., & Dicke, M. (1996). Plant-carnivore mutualism through herbivore-induced carnivore attractants. Trends in Plant Science, 1(4), 109-113.

Sakhalin Rock

Sakhalin RockOki Dub Ainu Band (music) / Morita Takahiro (director)
Ainu music + stop-motion + collage + maps + black and white photographs + Cyrillic script = AWESOME GEEKTASTICNESS

Black Fridays

GEK1517 Tutorial One: Consider the problem: Is there at least one Black Friday (Firday the thirteenth) in every year? How would you approach such a problem?

a. Of course, being a kid spoilt with the power of computers, the first thing I thought of was of course to devise a computer algorithm which will sift through the calendars of past, present and future years until it arrives at a Black-Friday-less year.

If there is one year where Black Friday does not exist, of course this will be fine. But if there isn't one, this method can never prove that every year must feature a Black Friday. "So you have tested a lot of cases! But have you tested all cases? No! What if the next year has no Black Friday? and so on ad infinitium.)

b. A better way would be to simplify the problem into patterns.
So I temporary f-ked the maths and went into empirical observation. From my handphone calendar, I observed that the 13th days in the months of January, February, etc. fell in this pattern:

{Wed Sat Sat Tue Thu Sun Tue Fri Mon Wed Sat Mon}

How to make sense of this pattern?
Recall that in non-leap years, the number of days in every month are the same.
So, as an example, January is always 31 days long.
It follows that 1 Feb is always 31 days after 1 Jan.
After which we can see that 13 Feb is always 31 days after 13 Jan.

However, you want to express this rule in days of the week (d.o.w.). So 31 days after Wednesday will be a Saturday, because

31 days = 4 times (7 days) + 3 days

Apply this to the pattern above and you can see that only the last term (+3 days) is needed: 13 Jan 2010 lies on a Wednesday, 28 days is exactly four weeks, so 28 days after 13 Jan is still on a Monday. We are only concerned with how the day of the week change, so the former term can boot it. And we write:

January -> February: 3 days
(to obtain the d.o.w for 13 Feb from 13 Jan, we skip forward 3 days in the week)

By this line of thought, Sunday + 1 is Monday.
So it makes sense to visualise the cycle of the week using a number line which looks like this:

Meanwhile, we obtain from the year 2010:
February -> March: 0 days
March -> April: 3 days
etc.
and we arrive at this twelve skip-forward values, from Jan->Feb to Dec->Jan

{3, 0, 3, 2, 3, 2, 3, 2, 3, 3, 2, 3, 2}

Be reminded that since number of days every January/February/etc. for different non-leap years are the same, these skip-forward values apply to all non-leap years.
How to make a conclusion from this array?
We take out the number line again, and put the month on the d.o.w its 13th day lands on, using the twelve skip-forward values for each month after January.
Anyway,

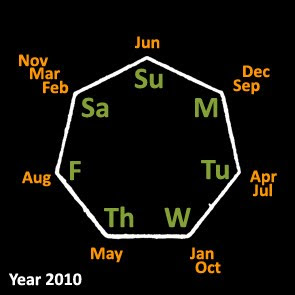All the days of the week are covered!
You'd be glad (or infuriated) that this says the same thing as the array

{Wed Sat Sat Tue Thu Sun Tue Fri Mon Wed Sat Mon}

But now it is clear that that it makes it obvious that no matter what day 13 Jan lies on in some other year, there will be a black friday somewhere down the year:

To solve for leap years, just take note that a leap-year February has one more day than a non-leap-year February. So the skip-forward value for February->March in a leap year is 1. The other values stay the same.

We see that even in a leap year, the 13th days of the month cover all days of the week. (What I did to introduce the gap of 1 between February and March was just to shift February and January one step earlier)


Yep, the leap year also covers all the days of the week.

[Spoiler: lecturer presented a one-size-fit-all-years solution which ignores February.]

To arrive at the lecturer's strong case, the only step we need to make is to shave of the superfluous months that crowd uselessly at a d.o.w.


The consecutive months of December to April are discounted, and since February is left out of consideration, the same diagram can demonstrate both leap and non-leap years.

-END OF DEMONSTRATION-

The Nabla Vector

Poor maths tutor. By the way he's going, it seems that he would fall asleep before the rest of the class does.
The syllabus is actually quite ok. One just has to get around all that stuff about the del operator (∇) which only looks intimidating. The rest is zooming in and out of the infinitesimal, as usual.


Analogy. I hate it when the notes gives such dry-as-dust statements like "the curl/divergence of a vector field F is defined by [formula]". O, how we will revel in the rote memory! Here I'll try a more helpful description on the concepts of gradient, divergence and curl.

The Mysterious Nabla vector ∇ (and applications thereof)
∇ is basically (∂/∂x)i~ + (∂/∂y)j~ + (∂/∂z)k~. It is not a vector in totally good faith, but it behaves like one and we treat it like one anyway (to hell with details).

Gradient: product of ∇ and a scalar field
Metaphor: Liken the scalar field f to altitude in a hilly area (say in Temburong).
Imagine that are a 2LT navigating your way to Lakiun Camp with your mates. At some point of time (and some point of f(x,y)) you decide to torture them by leading them directly upslope. The gradient of the terrain is a vector that points to the direction of "directly upslope".

Note: A force field which is a gradient of a scalar is called a conservative force because it "conserves mechanical energy". But why does it have to be that (F~ = ∇f) ⇔ (F~ is conservative)? This needs some looking into.

Divergence: dot product of ∇ and a vector field
Metaphor: Liken the vector field to a crowd of people moving with various velocities.
Imagine a crowded city square in Xi'an. At this instant, someone unearths a timed explosive at A, and someone else unearths an ancient national treasure at B. The crowd near point A will scramble away from A out of fear, while those near point B will scramble towards B out of curiosity. We say that the divergence at A is positive while the divergence at B is negative.

Curl: cross product of ∇ and a vector field
Metaphor: Liken the vector field to the surface of a rough sea.
Imagine going to fish in your new yacht when suddenly a freak storm arrives and your boat is send tossing and turning. The curl of the surface of the sea at (x,y) is the force that sends your boat turning (rather than tossing).

Note that curl of a conservative field (∇f) is zero. This is because
curl(∇f) is ∇×∇f.
∇ and ∇ are "parallel"
so ∇×∇ is 0
curl(∇f) is ∇×∇f, which is zero times f, which is zero.
Weird! And questionable.

A small note for GEK1517

Concierto de Aranjuez
2nd movement: Adagio
Joaquín Rodrigo (Comp.) / Narciso Yepes (12-stringer)
Dear visitors, I have noticed that many of you wind up on this site by searching for GEK1517 Mathematical Thinking tutorials. You might have been dismayed because so far I have been documenting only all the silly trivial stuff.

Yes, a GEK1517 tutorial solution set is in the plans.
No, it will not be the lecturer's solutions. Lifting and presenting them will totally spoil your pleasure (and that of all future generations) of going for tutorials. They shall be my own independent attempts.

Meanwhile, You'd be glad to know that a compilation of (own) tutorial answers can be found at Aldrian Obaja's website. I personally don't find his presentation very helpful, but it is a good source of encouragement for those who despair on the impregnability of the questions.

Ultimately, the best way around the tutorials is to try the questions yourselves, and then post it online afterwards, like the braggart I am going to be.

The Alternative Invasive Species

Imagine if I ditched the insidious but boring Imperata cylindrica (L.) Beauv. for an invasive species with an aspect that would better capture the public imagination:

Didymosphenia geminata (Lyngbye) M. Schmidt!
[Source]

Also considered: 2 species of ant, 2 species of snail, 1 snail-eating flatworm, 1 comb jellyfish, common mynah, sparrow, rock pigeon, rabbit, brown rat and brown trout.

Now back to work.

Freshman Journal 1.1.8

Year 1, Semester 1, Week 8
This week was not a very good week. Had problems like not being able to fall asleep at night, lack of motivation to work and the like nonsense.

Sisters got Confirmed in Church today, in an event graced by the Archbishop. Marie got herself a new middle name, after a saint famous for cracking a stupid joke while he was being martyred.

I. Modules

Ia. WP2201I Messing With Nature: Unintended Consequences
I was sifting through the mound of information found concerning lallang/cogongrass online. Some of the useful info that needs the unearthing:

Cogongrass, properties
Cogongrass in SE United States, status, methods of eradication
Cogongrass in Asia and Africa, status, methods of eradication
Cogongrass in South America, yada yada
Wickedly ingenious extermination methods

I don't like it when they ask me to purchase the article!

Ib. MA1505 Mathematics I
I am in the habit of drawing graphs in order to make sense of the equations, determinants or whatever nonsense they teach in class. Even though the derivations may not work out, the exercise tends to ram the equations deep into my memory.

Ic. GEK1517 Mathematical Thinking
W. Byers, author of How Mathematicians Think, gives an unpleasant revelation that Calculus is not really rigorous mathematics.

Id. PC1431 Physics IE
I am so saddened by the mid-term results that I have not touched this subject for one week. Ok, I know that this is not the best way to approach the problem.

II. CCA

IIa. MIR
10km run last Tuesday. Did not fare well. Alas, all the knolls of Upper Kent Ridge Road now bear testament to my drop in fitness. I need to train more as my schedule would allow. Eating more could also help. AHAHAHAHA.

IIb. GENUS
The last 2 weeks saw insane Saturday practises. Despite this, I decided that practising in Prime II was not insane enough and asked for a switch to Alto I, a proposition I regretted making almost immediately. Thankfully, it did not get through.

A couple of defectors from Alto I joined our section on Saturday, bringing up the strength to 20.

Freshman Journal 1.1.7

Year 1, Semester 1, Week 7.
Apologies for extreme randomness

I. This Picture is Actually From Week 5

8 September 2010: Guitarras Viva (The Noob Section)
II. MIR Publicity Campaign Now Public


III. Mid Term Tests
I aimed for full marks in Maths/Physics/Chemistry but it is not likely that I will get a perfect score for any of those in this fateful week.
Please do not feel alarmed. Ideally, everyone should strive for a perfect score. Realistically, normal people will miss the mark. Everyone will nevertheless enjoy for themselves, in return, the infinite joys of mugging.

IV. Mugging
Don't overdo the neurotism. Listen to relaxing instrumental music while studying, and by "instrumental" I mean of course to rule out anything involving synthesisers.

V. WP2201I Expository Essay

[source]
I forgot to elaborate; the topic of WP2201I is Invasive Species. For our third paper, we will be writing a 1000-word essay on an invasive species of our choice. My choice is the Lallang, a.k.a. cogongrass, or kunai, or 茅萱, cỏ tranh, etc.

Reasons for choosing this species fella:
1. Wide geographical spread:
All around the world, below the subtropical latitudes; O Lallang, the sun shall never set upon thy domain.
2. High profile:
Overtook Kudzu as the number 1 dick weed in the southern US, occupying 1.5 million acres of land as compared to Kudzu's 1.0 million acres.
3. Paranormal allusions:
Tendency to Spontaneous Combustion.
4. It's a plant
Plants are very underrated things, if only for them being boring and not inviting dramatic intepretation as readily as other, more metazoan invasive types, like rabbits.


You realise that Watership Down is largely about bunnies, and not at all about the noxious indestructable invasive weed pictured in the foreground.

Also,
[Episode 1. Disclaimer: for time-wasting purposes only]
VI. An Appropriate Freshman Attitude
Let your hair down because now you have your hair. Leave your past behind. Forget the grand achievements you have had, the stories you have accumulated, the knowledge you have gathered under your belt. Forget about looking cool and looking smart: Be childlike so that you can fill your heart with a sense of wonder, and a thirst for knowledge. Be humble so that you may find your place, and to open up to new possibilities. You have come to school again and you have come into this world as a nobody, as fresh as a newborn child. And being a newborn child, this is no time to act all stuck-up.

VII. A Response to the Recently-Announced Exoplanet Survey on Gliese 581g


What, it doesn't rotate?!