Lo, how a Rose e'er bloomin'

1. Es ist ein Ros' entsprungen (adap. Praetorius 1609)
2. Nu är det jul (Trad.)Ale Möller (Mandola and flute)Lisa Rydberg and Esbjörn Hazelius (Violins)Roger Tallroth (Bouzouki)Olle Linder (Double Bass)A Blessed Christmas to all in this sainted year 2010!

Sjömansvisan

My first complete transcription on Sibelius 5, a slow-ish sailor's ballad:

Title: Sjömansvisan (The Sailor's Song)Lyrics: Traditional Swedish
Music: Ulrika Bodén
As performed by: Ranarim (Sweden)
Code: T01.se / [see complete PDF]

Lyrics:

Skeppet seglar och vinden blåser
nu hissar vi våra ankar
vi ska segla till vännen kära
den vi har i våra tankar
Räck mig nu den snövita handen
om du vill bliva min kära
och vi ska tacka både fader och mor
om vi varandra skall äga

Dagen lider och solen skrider
och stjärnorna tändas upp igen
inte kan jag till vännen komma
varken åka, rida eller gå
Räck mig nu den snövita handen
om du vill bliva min kära
men jag får vänta till sol och sommardag
då jag seglar över böljan blå
Translation:

The vessel sails and the wind blows
Now we raise our anchors
We’ll sail to our beloved,
who is in our thoughts
Reach out your snow-white hand
If you will be my love
We shall thank both Mother and Father
if we shall have each other

The day passes and the sun moves across the sky
The stars are again lit
I cannot reach my beloved,
neither ride nor wander
Reach out your snow-white hand
If you will be my love
But I must wait for sun and summer days
to sail the bounding main

The Aranjuez Diaries

Concierto de Aranjuez 3rd movement: Allegro Gentile
Joaquín Rodrigo (Comp.) / Narciso Yepes (12-stringer)
Before each Wednesday or Friday evening lecture, Prof Leung liked to play Concierto de Aranjuez from Youtube as a kind of mood setting. Usually only movements 1 or 2 were played, but the third movement is my favourite, so here you go.

List of Solutions in GEK1517 Disclaimer: These are my own solutions, not the ones derived in class; so if I couldn't get a solution or the lecturer's solution is the same as mine, I would not post it. It should follow that the demonstrations are imperfect and not final.Tutorial 1: Black Fridays
Tutorial 3: Cracking Tiles
Tutorial 6: Fibonacci's Rabbits
Tutorial 6: Turtle Crawl
Tutorial 8: Szymborska's Utopia
Examination: Proving the Obvious

Miscellany: Application to MA1505: The Nabla Vector (use of metaphors)
Application to MA1505: Theorems of Vector Calculus (graphical demonstration)
Quote: Bishop George Berkeley (how not to learn science)
Quotes: Polanyi, Annan and Byers (somewhat random)
Concierto de Aranjuez, second movement

About the Course A course in the ideas behind breakthroughs in mathematics. In the course, complicated ideas are broken down into simple ones and presented as the mathematicians would have imagined it. This idea is mirrored in the test/exam/tutorials, where one arrives at proofs using guided instructions. This course reveals the joy of mathematics. Despite this, it probably put off some people from maths forever.

Because some things cannot be unlearnt, the ideas of GEK1517 has stuck on me and follows me wherever I go, surfacing occasionally and unexpectedly in my other modules (Calculus, physics, chemistry and even writing!).

Proving the Obvious

GEK1517 Examination / Question 1:

(i) Preface: Peano's Axioms
UT: The set of all natural numbers ℕ = {1, 2, 3, ...}
UT: 1
UT: Successor (here denoted by ')
(A1): 1 is a natural number
(A2): If a number a is a natural number, its successor is also a natural number
(A3): 1 is not the successor to any natural number
(A4): If two numbers have the same successor, they are the same number.
(A5): If 1 is a member of set K, and if for every natural number a, a is a member of K implies that a' is a member of K, then K is the set of all natural numbers. (Mathematical Induction).
The proofs in the following also feature reflexive equality (Ar) strongly. This is the first axiom in Peano's original list of axioms but was omitted from class notes. Essentially, it means x = x.

(ii) In the Peano axiomatic system for natural numbers, addition '+' is given inductively by the following two properties.
(+₁): a + 1 = a' for a ∈ ℕ
(+₂): a + b' = (a + b)' for a, b ∈ ℕ
Using (+₁), (+₂), and mathematical induction, show that
1 + a = a + 1 for all a ∈ ℕ

Solution:
Let P(a) denote (1 + a = a + 1 for all a ∈ ℕ)
P(1): 1 + 1 = 1 + 1 (true because (Ar))
P(k): 1 + k = k + 1 (force true)
P(k'): 1 + k' = k' + 1
(+₁): 1 + k' = (k + 1) + 1
(+₁): 1 + k' = (k + 1)'
(+₂): (1 + k)' = (k + 1)'
(A4): 1 + k = k + 1 (true because P(k))
(A5): Statement proven for for all a ∈ ℕ

Lemma 1 (L1): Commutativity of +
To prove: a + b = b + a for all a, b ∈ ℕ
Let P(a) denote (a + b = b + a) , b ∈ ℕ
P(1): 1 + b = b + 1 (true because (ii))
P(k): k + b = b + k (force true)
P(k'): k' + b = b + k'
(+₁): k + 1 + b = b + k'
(ii): k + b + 1 = b + k'
(+₁): k + b' = b + k'
(+₂): (k + b)' = (b + k)'
(A4): k + b = b + k (true because P(k))
(A5): Statement (L1) proven for for all a, b ∈ ℕ

(iii) In the Peano axiomatic system for natural numbers, multiplication '×' is given inductively by the following two properties.
(×₁): a × 1 = a for a ∈ ℕ
(×₂): a × b' = (a × b) + a for a, b ∈ ℕ
Using (×₁), (×₂), and mathematical induction, show that
a × 2 = a + a, and
a' × b = a × b + b for a, b ∈ ℕ

Solution part 1:
Let P(a) denote (a x 2 = a + a)
P(1): 1 × 2 = 1 + 1
What is 2? Take 2 = 1' (oh no...)
P(1): 1 × 1' = 1 + 1
(×₂): (1 x 1) + 1 = 1 + 1
(×₁): 1 + 1 = 1 + 1 (P(1) true because (Ar))
P(k): k × 2 = k + k (force true)
P(k'): k' × 2 = k' + k'
(2 = 1'): k' × 1' = k' + k'
(×₂): (k' × 1) + k' = k' + k'
(×₁): k' + k' = k' + k' (true because (Ar))
(A5): Statement proven for for all a ∈ ℕ

Solution part 2: Commutativity of ×
Let P(b) denote (a' × b = (a × b) + b), a ∈ ℕ
P(1): a' × 1 = (a × 1) + 1
(×₁): a' = a + 1
(+₁): a' = a' (true because (Ar))
P(k): a' × k = (a × k) + k (force true)
P(k'): a' × k' = (a × k') + k'
(×₂): (a' × k) + a' = (a × k) + a + k'
using P(k): (a × k) + k + a' = (a × k) + a + k'
(+₂): (a × k) + (k + a)' = (a × k) + (a + k)'
(L1): a + k = k + a
so (a × k) + (a + k)' = (a × k) + (a + k)' (true because (Ar))
(A5): Statement proven for for all a, b ∈ ℕ

Colophon:
The idea: you must forget all your arithmetic before you tackle this question. There is no arguing that "everyone knows" a+b = b+a; the only way is to prove it from the given axioms and properties. This is the intellectual equivalent of bailing out from a plane into the rainforest and building civilisation from the bottom up, right down to foraging for food, starting a fire, etc.

This is the first and only real proof in the series... I hope this is rigorous enough, and I hope the formatting makes it clear to follow (Facebook users please allow yourselves to be redirected to the "original post")

Regrettably, I did this only today, when the dust has settled over the exam period and freedom, merriment and general goofing off is in order. Never mind, enjoy the holidays folks.

Freshman Journal 1.1.R2

USP Chatterbox
The hell was I thinking when I said no? USP is like some heaven on earth!

Revision Round-up
Maths
Made understandable: L'Hopital's Rule, Fourier coefficients, Green/Stokes/Gauss Theorems
What still needs to be looked into: Taylor coefficients, Hessian determinant, Vector dot/cross products

Physics
Done: Flowcharts for Newtonian Mechanics + Thermodynamics
Made understandable: Adiabatic free expansion (!!!!!)
I don't need to take out notes anymore AHAHAHA

Chemistry
Memorise stuff.

Mathematical Thinking
Philosophise.
Panic.

Szymborska's Utopia

GEK1517 Tutorial 8 / Question 1: Discuss the metaphors and associations used in the following poem 'Utopia' by Ms. Wisława Szymborska (Nobel Laureate in Literature, 199[6]).

Ms. Wisława Symborska
I am sorry to find out, after a brief background search on Ms. Symborska, that her life displayed all the dweeb-patterns as seen in Jaromil, the Milan Kundera character I love to deride so much. This is not a very good poem; it makes an awkward reading, but the mathematical ideas expressed makes it relevant to the module and especially interesting.

This is reason enough for me to offer a free-rambling intepretation, so if you'll indulge me for one post--

Island where all becomes clear.
1. The island is Mathematics. Welcome to the world of Maths!

Solid ground beneath your feet.
2. "Solid ground" undefined terms, axioms of mathematics(?)
3. "Solid ground" everything else is groundless (?)

The only roads are those that offer access.
4. The only questions asked are constructive
aside: There are roads that "don't offer access"?!

Bushes bend beneath the weight of proofs.
5: Proofs open up new paths through ignorance (foliage)

The Tree of Valid Supposition grows here
with branches disentangled since time immemorial.
6: This vaguely refers to speculation, or intelligent guesses (?)

The Tree of Understanding, dazzlingly straight and simple,
sprouts by the spring called Now I Get It.
7: This vaguely refers to the "eureka" moment as cherished by all bona fide nerds.

The thicker the woods, the vaster the vista:
the Valley of Obviously.
8: At first I thought this was stating the obvious, but then
9: Imagine looking across the valley, specifically at the trees on the other side. You can see all the features there very clearly, but you have not found a way to get to the other side! For that, you will need some "[bush bending] beneath the weight of proofs."

If any doubts arise, the wind dispels them instantly.
10: Possibility 1. The atmosphere discourages you from thinking critically.
11: Possibility 2. In this Utopia, nothing stays unknown or unresolved for long.

Echoes stir unsummoned
and eagerly explain all the secrets of the worlds.
12: Because you get all these dead mathematicians whispering stuff into your ears.

On the right a cave where Meaning lies.

On the left the Lake of Deep Conviction.
Truth breaks from the bottom and bobs to the surface.
13: Conclusions comes only sporadically. Once it is freed from the lake bottom, it bobs quite readily to the surface. Maybe this means that the first step is always the hardest.

Unshakable Confidence towers over the valley.
Its peak offers an excellent view on the Essence of Things.
14: Possibly uncharacteristic praise of dogmatism.
Corollary to 14: Possibly, after all this doubting and questioning and decosntruction of knowledge, being a good mathematician still takes a definite serving of balls and tough braincases.

For all its charms, the island is uninhabited,
and the faint footprints scattered on its beaches
turn without exception to the sea.
15: No one makes mathematics his/her whole reality.

As if all you can do here is to leave
and plunge, never to return, into the depths.
16: Corollary to (15).

Into unfathomable life.
17: Classical dweeb sign-off!
18: Real life is always where we end up in and what we are more used to, even though it is more complicated and much harder to understand than mathematics.

--END OF EQUIVOCATION--

Please comment if you have some better way of deciphering the above poem!

Turtle Crawl

GEK1517 Tutorial 6 / Question 2.
Consider the turtle's movement:
F means advancing 1 unit in the firection of the turtle's head:
+ / - means, respectively, turning the turtle's head to the right / left by d degrees - the position of the turtle remains unchanged.
Take d = 90˚and start with F + F + F + F (0[th] iteration). In the subsequent steps, let the rewriting rule be
F ↦ F - F + F
(a) Sketch the first two iterations.
(b) It is observed that in the first few iterations, the turtle always returns to the same position where it starts. Does this hold for all iterations? Present the key ideas critically and carefully to support your answers.


Key Ideas:
1: As given, Iteration 0 produces a closed loop.

2: (1) applies because in Iteration 0, F is reproduced 4 times, then joined together so that each F is rotated 90 degrees to the right w.r.t. the previous F. This forms a closed square loop.

3: In every subsequent iteration, the instances of F produce identical segments.
F + F + F + F
↦ F' + F' + F' + F'
↦ F" + F" + F" + F" ...

4. In every subsequent iteration, we find 4 identical segments joined end on end, each one rotated 90 degrees right w.r.t the previous segment. This also forms a closed loop.
Fⁿ + Fⁿ + Fⁿ + Fⁿ

4. If (4) is shown to be true, proposition holds for all iterations
Summary: (1) is given, (1) requires (2), (2)⇒(4) proven, ⇒ proposition holds

-- END OF DEMONSTRATION --

Iterations 3 and 4 for your enjoyment

Fibonacci's Rabbits

GEK1517 Tutorial 6 / Question 1.
Starting with the letter b, consider the rewriting rules
b → a; a → ab.
For example, the first few 'words' formed by the above rewriting rules are
b, a, ab, aba, abaab, abaababa, ...
Let C(n) be the number of letters in the n-th word (n is a positive integer). For instances [sic],
C(1) = 1, C(2) = 1, C(3) = 2, C(4) = 3, C(5) = 5, C(6) = 8, ...
Prove that
C(n+1) = C(n) + C(n-1)
for all integers n ≥ 2. (Caution: Math. induction may not work well here.)

Spoiler: Lecturer's solution is more elegant, so please bear with me here.

Let number of 'b's in n-th word: B_n.
Let number of 'a's in n-th word: A_n.

Because of the rewriting rules b → a; a → ab.
'b's in a word is generated only from 'a's in the previous word
∴ B_n = A_n-1
'a's in a word is generated from both 'a's and 'b's in the previous word.
∴ A_n = A_n-1 + B_n-1

Now total number of letters in n-th word is C(n)
Total number of letters in n-th word is sum of 'a's and 'b's.
∴ C(n) = A_n + B_n
now
C(n-1) = A_n-1 + B_n-1 = A_n
C(n+1) = A_n+1 + B_n+1

To show that C(n+1) = C(n) + C(n-1), express all terms in A_n and B_n.
C(n+1) = C(n) + C(n-1)
⇒ A_n+1 + B_n+1 (LHS)
= A_n + B_n + A_n = 2A_n + B_n (RHS)
∵ B_n = A_n-1,
B_n+1 = A_n.
∵ A_n = A_n-1 + B_n-1,
A_n+1 = A_n + B_n.
Sub back into LHS:
LHS = A_n + A_n + B_n
= 2A_n + B_n = RHS.

-- END OF DEMONSTRATION --

Chimness

Self-respecting intellectuals listen up:
If someone says your ideas are "chim", do not take it as a compliment.
It is an INSULT.
Go back home and sleep on a nettle bed.
Hang a snake gall from the ceiling or something to remind yourself of the shame you had to bear.
Later on, make a comeback by presenting your ideas more clearly and intuitively.

Somewhat Random Quotables

It is only in the popular mind that knowledge equates with facts.
That is of course flattering, since facts are incontrovertible.
But it is also demeaning, since facts are meaningless;
they contain no narrative.

-- POLANYI John Charles

The idea that there is one people in possession to the truth,
one answer to the world's ills,
or one solution to humanity's needs,
has done untold harm throughout history, especially in the last century.

-- ANNAN Kofi (2001)

The certainty of mathematics is different from the certainty one finds in other fields; it is somehow purer and therefore more powerful. To be certain is to know. What an extraordinary feeling it is to know and to know that you know! What strength there is in that position! What confidence one has when one sees into the truth of some mathematical theorem! The angles of a triangle add up to two right angles. It is not a matter of "probably," "almost always," "in our experience," or "as far as we know." None of these usual caveats apply -- there is no quibbling. If you are not completely certain, if you have the slightest doubt, then you just don't get it. Mathematical truth has this certainty, this quality of inexorability. This is its essence.

-- BYERS William (2007), How Mathematicians Think
I just love it when mathematicians get emotional.

Theorems of Vector Calculus

Notes on the physical meanings of the theorems of Green, Stokes and Gauss covered in MA1505 Chapter 10

Introduction
Those who are familiar with the Mathematics module (the one specially designed to traumatise engineering freshmen) would readily identify the following formulas to be the point where it all starts to fall apart (ignoring Fourier series).

At first glance, these formulae all seem to be coincidence, as what can there be to relate integration over a line with integration over a surface, or to relate integration over a surface with that over a volume? The notes give no helpful explanation either... but the underlying idea is quite simple to understand!

Disclaimer
This following is a demonstration, not a proof. The goal is understanding, not certainty. If one is interested, there are pretty good proofs for Green's theorem as well as the theorems of Stokes and Gauss (TAYLOR Peter D., 1992).

Idea
Special case assumption: When you sum up small loops, they become one big loop.
As seen in this tile of four loops, the interior arrows cancel out and leave the outer boundary of the loop (which has nothing to cancel out with).

We apply this principle everywhere else rather thoughtlessly. Does anyone remember Carnot engines from Physics PC1431? How do you reduce a reversible process to a sum of Carnot cycles?
Yes.
General assumption: The interior boundaries cancel out.
The important thing is that the R.H.S of the three theorems deal with summing up quantities for which the internal boundaries cancel out each other. This is why summations (integral) over a plane/volume can equate to summations over the plane/volume's outer boundary.
This general assumption is necessary to bring Gauss' Theorem into the discussion.

Stokes:A Loopy Proposition
Aside: In practise, it is easier to use Green's theorem to prove Stokes' Theorem rather than the other way round, for an idea how this is done, please refer to Thomas' Calculus (12th ed.), Chapter 16. However, for this section, only Stokes' theorem will be demonstrated (Green's theorem follows as its 2-D speical case, a fact which you may have learnt in class).

The basic idea of Stoke's theorem is to add up the curl (small loops) of the vector field to a closed-path integral (the big loop).
(1)It can be seen that in a 3-D space, many different surfaces can share the same boundary.

(2)As follows from the assumption, any closed loop can be split up into smaller loops, and then split up into even smaller loops, and so on ad infinitium. The sum of these loops, as expected, equals the big loop i.e. the boundary of the surface. This ensures that even for different surfaces, the integral can be the same if the surfaces share the same boundary!

(3)If the big loop can be thought of as the sum of infinitesimal loops, we can approximate each infinitesimal loop to the curl at a point (normal to the surface).

What is the meaning of curl?
Curl is what textbooks describe as "circulation density". Basically, it is how much vectors swirl in the immediate neighbourhood of a given point. The curl vector points upwards if the net circulation is counter-clockwise from above, and vice versa.

The big last step: Approximating infinitesimal loop to curl
After obtaining your infinitesimal surface dS, it is time to match the 2 quantities
(1) Line integral over the infinitesimal loop
(2) Curl over the point

Admittedly, I have not found a way to settle this step yet, but here are 2 important observations:

(1) The quantities a)line integral over infinitesimal closed loop and b)curl derive their values from the same 4 vectors in the neighbourhood of small surface area dS.

(2) Only the components of a) and b) aligned with the surface of dS are taken:


Gauss: Analogy using Jigsaw Pieces


The cutest formula in the bunch also looks the most devastating, not least for its prominent feature of a triple integral. However, the fact that features a divergence operator rather than a curl operator makes it infinity times friendlier to the brain.

Basically, what is says is:
The volume flow rate over a closed surface
is equal to
The net divergence in the volume enclosed by the surface.

What is the meaning of divergence?
Divergence at a point is a measure of the net tendency of nearby vectors to point inwards into the point or outwards away from the point.
Basically,

The cube is a small volume dV in the space enclosed in the surface.
In the jigsaw analogy, we simplify each small volume dV into a jigsaw piece.
The tendency for outflow at one edge, contributing to positive divergence, is represented by a protruding knob.
The tendency of inflow at one edge, contributing to negative divergence, is represented by a hole.

The big step: Cancelling out the interior boundaries
The boundaries must cancel out in between volumes. This is because any vector which contributes to positive divergence in one small volume dV also contributes to the same amount of negative divergence in an adjacent dV, and vice versa.


This is the same as saying in the jigsaw analogy that 2 adjacent jigsaw pieces fit each other smugly.

The "divergence" is found by adding up the knobs (1 per knob) and holes (-1 per hole) along the edge. The "divergence" in the result sum can be thought of as the sum of the "divergences" in the individual jigsaw pieces. It can also be thought as the sum of knobs and holes along the edge of the result (i.e. by giving it a count).

A final observation: The key to understand why Gauss' Theorem works is the same key to understand why a completed puzzle always has straight edges (a particular case of zero divergence) even though all the pieces in it are jaggedy!

-- END OF DEMONSTRATION --

Freshman Journal 1.1.12

Maths
Maths tutorial this week has disappeared. I don't know if the venue had shifted without warning, but when I arrived there 15 minutes late, there wasn't a class in E1-06-03.
Lecturer went into an exam-question-crunch frenzy, which for all his virutosity is totally useless for revising concepts.
I am into Stokes' Theorem at the moment, partly to distract myself from the existential horror of never being able to get a girlfriend, and partly because it is awesome.
What secrets doest thou hide? O impenetrable formula!

Physics
Completed the Mastering Physics questions. Considering to finish the non-compulsory questions on the site along with those in the tutorials, but I hate doing stuff on the computer.
I realise that our Physics tutor (Ms. Qiu Leiju) is one of the best tutors I've had for the semester.
Syllabus sped in and out of Thermodynamics for the past weeks. The flame of physics was rekindled in me at the point when it went to the Second Law. Holding that disorderliness is ever-increasing and that all energy is eventually useless, this law is a sobering reminder of the mortality of humankind. Who knew that such a profound result could arise from the obscure fumblings of some 19th-century nerds?

Writing
The last lessons were concluded with 2 sessions of final presentations, a group photograph, and some wicked delicious cookies baked for us by our tutor, Mr Griner.

Chemistry
The whole syllabus of CM1417 is so random and counterintuitive that I find it quite unsettling that I will have to face the same sort of courses for all my subsequent semesters.

Cracking Tiles

GEK1517 Tutorial Three / Question Two: Suppose that there are m×n unit square tiles arranged into a rectangle (a square if m=n; here m and n are positive integers). A crack appears as a diagonal line of the rectangle (see the figure for m=3 and n=5. Speculate on the number of tiles that are ruined and need to be replaced. (Your answers should be in terms of m and n). Provide arguments to support your answers.


Step I: Panic

Step II: After calming down, try the shit out of as many lower values of m and n you could be bothered with.


Assume that the number of tiles follow a rule; nail the rule down to a symbol.
Number of tiles damaged = D(m,n)

Make the following observations which may or may not come useful later on.

m and n are interchangeable.

Extreme case I: Thin rectangle

Extreme case II: Square

After a bit of trying, arrive at the formula
D(m,n) = m + n - 1
which works for the largest number of the cases (including Extreme I cases)
Group cases according to how well they conform to D = m + n - 1 (mirror images are ruled out as trivial)


It should be very clear now what differentiates the two groups.
The left group ("conformist" rectangles) have cracked tiles of continguous shape. The cracks do not pass through a point in between tiles.
The right group ("nonconformist" rectangles) have cracks that pass through a point (or points).
Somehow, passing through a point affects the crack count!

For curiosity's sake, have a closer look at the nonconformist group.


The nonconforming rectangles do not follow a single rule! Evidently, something has to be found out about this group that dictates the D(m,n).

Step III: Observe that every crack starts and ends on a point.

Observe that, if the crack passes through a point in a middle of a rectangle, you can break a smaller rectangle from it with that middle point as a new (top-right or bottom-left) corner. We take bottom-left:


Observe that, if the new rectangle also has the crack passing through a point between tiles, the process can be repeated until there is no point.


A rectangle where the crack does not pass through a point is a conformist rectangle.
We have demonstrated that a nonconformist rectangle can be reduced to a conformist rectangle.

How do you get back the nonconformist rectangle?
Every conformist rectangle, a series of nonconformist rectangles can be constructed by replicating the conformist x times along the crack's diagonal:


What is the D for a rectangle of length xm and height xn?
It is quite clear that this quantity D for a nonconformist rectangle can be taken apart into the sum of cracks for x conformist rectangles.


We arrive at
D(xm,xn) = xD(m,n)
for nonconformists, where D(m,n) is of a conformist rectangle
Which, owing to D(m,n) = m + n - 1, becomes
D(xm,xn) = xD(m,n) = x(m + n - 1) = xm + xn - x

Step IV:
Observe that in nonconformist rectangles (D(xm,xn) = xm + xn - x) width and height have a common factor x
Observe that in conformist rectangles (D(m,n) = m + n - 1) the width and height have no common factors other than 1.
Observe that D(m,n) = m + n - 1 is equivalent to D(1m,1n) = 1m + 1n - 1, which is just a special case for the nonconformists' rule (x = 1).
Observe that x is the highest common factor (h.c.f) between the width xm and height xn; since m and n have no common factors, the common factors include x and possibly a number smaller than x which is also a factor of x (x is still the highest).

Obtain the unified rule for all rectangles of width m and height n:
D(m,n) = m + n - (h.c.f of m and n)
Verify that rule applies to all cases presented above.

--END OF DEMONSTRATION--

Addendum: Ruohan's description of a proof
Set A {(a, an/m), where 0 ≤ a < m}.
Set B {(bm/n, b), where 0 ≤ b < n}.
Each point in A and B correspond to a cracked tile to the right of the point itself. The answer would then be A ∪ B = A + B - (A ∩ B).
Solving A ∩ B would then be solving the integer pairs for an = bm.

Lacuna: I asserted that a nonconformist rectangle be formed by duplicating the same conformist along the crack. I did not explain why a different conformist can not be used. To do so, I may slip into a circular argument.

Spoiler: Lecturer touched on how to count the cracked tiles, and did not arrive at the expression m + n - 1 by accident like I did.

Bishop George Berkeley

"Men learn the elements of science from others;
and every learner hath a deference more or less to authority,
especially the younger learners,
few of that kind caring to dwell long upon principles,
but including rather to take them on trust:
And things early admitted by repetition become familiar:
And this familiarity at length passeth for evidence."

-- A Defence of Freethinking in Mathematics (1735)

The Chemistry of Plant Communications

Somehow, plants show up very frequently in my first semester. First lallang for WP2201I, now plant pheromones for CM1417. I can't put a finger on what is really going on despite having chosen the topics myself.

Picture taken from:
Takabayashi, J., & Dicke, M. (1996). Plant-carnivore mutualism through herbivore-induced carnivore attractants. Trends in Plant Science, 1(4), 109-113.

Sakhalin Rock

Sakhalin RockOki Dub Ainu Band (music) / Morita Takahiro (director)
Ainu music + stop-motion + collage + maps + black and white photographs + Cyrillic script = AWESOME GEEKTASTICNESS

Black Fridays

GEK1517 Tutorial One: Consider the problem: Is there at least one Black Friday (Firday the thirteenth) in every year? How would you approach such a problem?

a. Of course, being a kid spoilt with the power of computers, the first thing I thought of was of course to devise a computer algorithm which will sift through the calendars of past, present and future years until it arrives at a Black-Friday-less year.

If there is one year where Black Friday does not exist, of course this will be fine. But if there isn't one, this method can never prove that every year must feature a Black Friday. "So you have tested a lot of cases! But have you tested all cases? No! What if the next year has no Black Friday? and so on ad infinitium.)

b. A better way would be to simplify the problem into patterns.
So I temporary f-ked the maths and went into empirical observation. From my handphone calendar, I observed that the 13th days in the months of January, February, etc. fell in this pattern:

{Wed Sat Sat Tue Thu Sun Tue Fri Mon Wed Sat Mon}

How to make sense of this pattern?
Recall that in non-leap years, the number of days in every month are the same.
So, as an example, January is always 31 days long.
It follows that 1 Feb is always 31 days after 1 Jan.
After which we can see that 13 Feb is always 31 days after 13 Jan.

However, you want to express this rule in days of the week (d.o.w.). So 31 days after Wednesday will be a Saturday, because

31 days = 4 times (7 days) + 3 days

Apply this to the pattern above and you can see that only the last term (+3 days) is needed: 13 Jan 2010 lies on a Wednesday, 28 days is exactly four weeks, so 28 days after 13 Jan is still on a Monday. We are only concerned with how the day of the week change, so the former term can boot it. And we write:

January -> February: 3 days
(to obtain the d.o.w for 13 Feb from 13 Jan, we skip forward 3 days in the week)

By this line of thought, Sunday + 1 is Monday.
So it makes sense to visualise the cycle of the week using a number line which looks like this:

Meanwhile, we obtain from the year 2010:
February -> March: 0 days
March -> April: 3 days
etc.
and we arrive at this twelve skip-forward values, from Jan->Feb to Dec->Jan

{3, 0, 3, 2, 3, 2, 3, 2, 3, 3, 2, 3, 2}

Be reminded that since number of days every January/February/etc. for different non-leap years are the same, these skip-forward values apply to all non-leap years.
How to make a conclusion from this array?
We take out the number line again, and put the month on the d.o.w its 13th day lands on, using the twelve skip-forward values for each month after January.
Anyway,

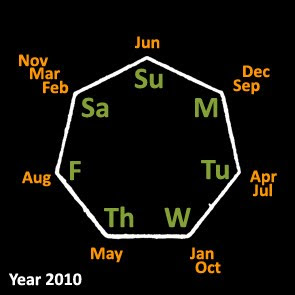All the days of the week are covered!
You'd be glad (or infuriated) that this says the same thing as the array

{Wed Sat Sat Tue Thu Sun Tue Fri Mon Wed Sat Mon}

But now it is clear that that it makes it obvious that no matter what day 13 Jan lies on in some other year, there will be a black friday somewhere down the year:

To solve for leap years, just take note that a leap-year February has one more day than a non-leap-year February. So the skip-forward value for February->March in a leap year is 1. The other values stay the same.

We see that even in a leap year, the 13th days of the month cover all days of the week. (What I did to introduce the gap of 1 between February and March was just to shift February and January one step earlier)


Yep, the leap year also covers all the days of the week.

[Spoiler: lecturer presented a one-size-fit-all-years solution which ignores February.]

To arrive at the lecturer's strong case, the only step we need to make is to shave of the superfluous months that crowd uselessly at a d.o.w.


The consecutive months of December to April are discounted, and since February is left out of consideration, the same diagram can demonstrate both leap and non-leap years.

-END OF DEMONSTRATION-

The Nabla Vector

Poor maths tutor. By the way he's going, it seems that he would fall asleep before the rest of the class does.
The syllabus is actually quite ok. One just has to get around all that stuff about the del operator (∇) which only looks intimidating. The rest is zooming in and out of the infinitesimal, as usual.


Analogy. I hate it when the notes gives such dry-as-dust statements like "the curl/divergence of a vector field F is defined by [formula]". O, how we will revel in the rote memory! Here I'll try a more helpful description on the concepts of gradient, divergence and curl.

The Mysterious Nabla vector ∇ (and applications thereof)
∇ is basically (∂/∂x)i~ + (∂/∂y)j~ + (∂/∂z)k~. It is not a vector in totally good faith, but it behaves like one and we treat it like one anyway (to hell with details).

Gradient: product of ∇ and a scalar field
Metaphor: Liken the scalar field f to altitude in a hilly area (say in Temburong).
Imagine that are a 2LT navigating your way to Lakiun Camp with your mates. At some point of time (and some point of f(x,y)) you decide to torture them by leading them directly upslope. The gradient of the terrain is a vector that points to the direction of "directly upslope".

Note: A force field which is a gradient of a scalar is called a conservative force because it "conserves mechanical energy". But why does it have to be that (F~ = ∇f) ⇔ (F~ is conservative)? This needs some looking into.

Divergence: dot product of ∇ and a vector field
Metaphor: Liken the vector field to a crowd of people moving with various velocities.
Imagine a crowded city square in Xi'an. At this instant, someone unearths a timed explosive at A, and someone else unearths an ancient national treasure at B. The crowd near point A will scramble away from A out of fear, while those near point B will scramble towards B out of curiosity. We say that the divergence at A is positive while the divergence at B is negative.

Curl: cross product of ∇ and a vector field
Metaphor: Liken the vector field to the surface of a rough sea.
Imagine going to fish in your new yacht when suddenly a freak storm arrives and your boat is send tossing and turning. The curl of the surface of the sea at (x,y) is the force that sends your boat turning (rather than tossing).

Note that curl of a conservative field (∇f) is zero. This is because
curl(∇f) is ∇×∇f.
∇ and ∇ are "parallel"
so ∇×∇ is 0
curl(∇f) is ∇×∇f, which is zero times f, which is zero.
Weird! And questionable.

A small note for GEK1517

Concierto de Aranjuez
2nd movement: Adagio
Joaquín Rodrigo (Comp.) / Narciso Yepes (12-stringer)
Dear visitors, I have noticed that many of you wind up on this site by searching for GEK1517 Mathematical Thinking tutorials. You might have been dismayed because so far I have been documenting only all the silly trivial stuff.

Yes, a GEK1517 tutorial solution set is in the plans.
No, it will not be the lecturer's solutions. Lifting and presenting them will totally spoil your pleasure (and that of all future generations) of going for tutorials. They shall be my own independent attempts.

Meanwhile, You'd be glad to know that a compilation of (own) tutorial answers can be found at Aldrian Obaja's website. I personally don't find his presentation very helpful, but it is a good source of encouragement for those who despair on the impregnability of the questions.

Ultimately, the best way around the tutorials is to try the questions yourselves, and then post it online afterwards, like the braggart I am going to be.

The Alternative Invasive Species

Imagine if I ditched the insidious but boring Imperata cylindrica (L.) Beauv. for an invasive species with an aspect that would better capture the public imagination:

Didymosphenia geminata (Lyngbye) M. Schmidt!
[Source]

Also considered: 2 species of ant, 2 species of snail, 1 snail-eating flatworm, 1 comb jellyfish, common mynah, sparrow, rock pigeon, rabbit, brown rat and brown trout.

Now back to work.

Freshman Journal 1.1.8

Year 1, Semester 1, Week 8
This week was not a very good week. Had problems like not being able to fall asleep at night, lack of motivation to work and the like nonsense.

Sisters got Confirmed in Church today, in an event graced by the Archbishop. Marie got herself a new middle name, after a saint famous for cracking a stupid joke while he was being martyred.

I. Modules

Ia. WP2201I Messing With Nature: Unintended Consequences
I was sifting through the mound of information found concerning lallang/cogongrass online. Some of the useful info that needs the unearthing:

Cogongrass, properties
Cogongrass in SE United States, status, methods of eradication
Cogongrass in Asia and Africa, status, methods of eradication
Cogongrass in South America, yada yada
Wickedly ingenious extermination methods

I don't like it when they ask me to purchase the article!

Ib. MA1505 Mathematics I
I am in the habit of drawing graphs in order to make sense of the equations, determinants or whatever nonsense they teach in class. Even though the derivations may not work out, the exercise tends to ram the equations deep into my memory.

Ic. GEK1517 Mathematical Thinking
W. Byers, author of How Mathematicians Think, gives an unpleasant revelation that Calculus is not really rigorous mathematics.

Id. PC1431 Physics IE
I am so saddened by the mid-term results that I have not touched this subject for one week. Ok, I know that this is not the best way to approach the problem.

II. CCA

IIa. MIR
10km run last Tuesday. Did not fare well. Alas, all the knolls of Upper Kent Ridge Road now bear testament to my drop in fitness. I need to train more as my schedule would allow. Eating more could also help. AHAHAHAHA.

IIb. GENUS
The last 2 weeks saw insane Saturday practises. Despite this, I decided that practising in Prime II was not insane enough and asked for a switch to Alto I, a proposition I regretted making almost immediately. Thankfully, it did not get through.

A couple of defectors from Alto I joined our section on Saturday, bringing up the strength to 20.

Freshman Journal 1.1.7

Year 1, Semester 1, Week 7.
Apologies for extreme randomness

I. This Picture is Actually From Week 5

8 September 2010: Guitarras Viva (The Noob Section)
II. MIR Publicity Campaign Now Public


III. Mid Term Tests
I aimed for full marks in Maths/Physics/Chemistry but it is not likely that I will get a perfect score for any of those in this fateful week.
Please do not feel alarmed. Ideally, everyone should strive for a perfect score. Realistically, normal people will miss the mark. Everyone will nevertheless enjoy for themselves, in return, the infinite joys of mugging.

IV. Mugging
Don't overdo the neurotism. Listen to relaxing instrumental music while studying, and by "instrumental" I mean of course to rule out anything involving synthesisers.

V. WP2201I Expository Essay

[source]
I forgot to elaborate; the topic of WP2201I is Invasive Species. For our third paper, we will be writing a 1000-word essay on an invasive species of our choice. My choice is the Lallang, a.k.a. cogongrass, or kunai, or 茅萱, cỏ tranh, etc.

Reasons for choosing this species fella:
1. Wide geographical spread:
All around the world, below the subtropical latitudes; O Lallang, the sun shall never set upon thy domain.
2. High profile:
Overtook Kudzu as the number 1 dick weed in the southern US, occupying 1.5 million acres of land as compared to Kudzu's 1.0 million acres.
3. Paranormal allusions:
Tendency to Spontaneous Combustion.
4. It's a plant
Plants are very underrated things, if only for them being boring and not inviting dramatic intepretation as readily as other, more metazoan invasive types, like rabbits.


You realise that Watership Down is largely about bunnies, and not at all about the noxious indestructable invasive weed pictured in the foreground.

Also,
[Episode 1. Disclaimer: for time-wasting purposes only]
VI. An Appropriate Freshman Attitude
Let your hair down because now you have your hair. Leave your past behind. Forget the grand achievements you have had, the stories you have accumulated, the knowledge you have gathered under your belt. Forget about looking cool and looking smart: Be childlike so that you can fill your heart with a sense of wonder, and a thirst for knowledge. Be humble so that you may find your place, and to open up to new possibilities. You have come to school again and you have come into this world as a nobody, as fresh as a newborn child. And being a newborn child, this is no time to act all stuck-up.

VII. A Response to the Recently-Announced Exoplanet Survey on Gliese 581g


What, it doesn't rotate?!

The Secret of Kells

The Secret of Kells
2009 Tomm MOORE and Nora TWOMEY (Dir.)
Bruno COULAIS (Music)
1 hour 15 minutes

It's not a normal classical animated feature when every frame looks like a flippen illuminated manuscript.

I have discovered Kíla

Kíla
Rossa, Rónán and Colm Ó Snodaigh, Dee Armstrong, Eoin Dillon, Seanan Brennan, Brian and Lance Hogan

Settling Scores

1. Scores should be settled as and when they arise, in order to preserve goodwill and minimise misunderstanding.

2. A score not settled is injustice allowed to happen. A score not settled is an insult to one's own willpower and to the other's moral standing.

3. A score is often foregone because one is afraid that the other will take offense. He forgoes the score to the expense of his own interests.

This is irresponsible behaviour; one has a limited capacity to which he is willing and able to shoulder the consequences of someone else's actions. He who makes it a habit will eventually give way himself, to the detriment of all around him.

The World is Rather Complicated

The world is populated with good people; people that have your best interests at heart, people who feel love, people who value friendship, people who find joy in helping others. When I believe this, I let my guard slip... and make bad decisions.

The world is populated with bad people; people who are irrational, people who have hidden selfish motives, people who are hateful, people who are lazy, people who have no sense of priority. When I believe this, I find it hard to tell what people are up to, and what they say often do not make sense. I admit too many possibilities, and fill up my mind with too much information... Eventually, something slips, and I make a bad decision.

Freshman Journal 1.1.4

Note: "Journal 1.1.4" denotes an entry from (Year)1.(Semester)1.(Week)4

I. Modules

Ia. MA1505 Mathematics I
Now because I take this GEK1517 module, MA1505 seems lame and pedantic.
However, this feeling is deceptive! When I do the tutorials, I keep needing the help of my 1-semester old answers (because in addition to crashing MA1505 lectures from February to April 2010, I also did the tutorial questions).
This can not continue. I must revise the concepts we learnt in class and make it intuitive in the most hardcore way imaginable.

Ib. GEK1517 Mathematical Thinking
I am wholly satisfied with this module and am enjoying all of its lectures and tutorials despite the possibility of me failing it at the end.
The lecturer Assoc. Prof. Leung is a difficult guy to talk to, although his lectures are entertaining.

Ic. PC1431 Physics IE
The lecturer talks with an accent I find unbearable. I cannot reproduce the accent for more than a few seconds without choking on my own tongue.
I MUST WORK HARDER ON THIS

Id. CM1417 Fundamentals of Chemistry
I want to quickly pwn this module because I get kind of embarrassed whenever I have to admit that I did not take H2 Chemistry for 'A' Levels.
To reiterate, the reason for not taking H2 Chemistry was pure stupidity.
Crashed a year 2 Chemistry lecture earlier this week with Brian, who told me that all the wonderful stuff on screen were covered by H2 Chem. Man, what have I missed all these years?

Ie. WP2201I Messing With Nature: Unintended Consequences
First graded assignment in on Thursday.
2 readings due tomorrow (guiltily as I write)

II. CCA

IIa. Mountaineering Club / MIR
I am now in MIR10 EXCO, understudy Publicity i/c.
I chose it not just because it sounds very slack, but also because I have experience in design ('A' Level credentials)!
The batch is small but new members keep coming in. Trainings consist of an endurance run on Tuesday evenings, speed training on Thursday evenings, and something fun and random on Saturday morning till noon.

IIb. Guitar Ensemble / GENUS
After 5 years in and out of guitar noobdom, I am performing in concert!
It's a late notice, but here are the details...

Wednesday 8 September
8pm
University Cultural Centre
Free Admission, Limited Seats!

My group's items are
Francis LAI arr. Koji KUBO: 13 Days in France
Sir Edward ELGAR arr. Masako OHASHI: Salut d'Amour

IIc. Catholic Students' Society / CSS
Infuriatingly, I have to skip lessons in order to attend the activities of CSS every week.
Attended a mass in LT17, School in Business on Friday, presided by Fr. Alex from Saint Joseph (Bukit Timah). It was the first time in my experience that the pews were higher in elevation than the sanctuary.

IId. Astronomy Club / NUSAS
Static.
With apologies to Kenneth!

I now recommend that although one tries their very best to be hardcore, their timetable will invariably disappoint them by clashing. One high-key and one low-key CCA is a good balance, and that is enough.

III. My weight
These weeks have seen increase. Evidently, my active lifestyle is not active enough. Will switch to a more masochistic regimen in short notice.

Needs some clarifying

Q. Are you Christian?
A. Yes.
Q. Which church do you go to?
A. Holy Cross.
Q. Where is it at?
A. Clementi.
Q. But isn't that a Catholic church?
A. Yes.
Q. So you're... Catholic-Christian?
A. Yes?

School Has Started

Enough of this denial. As I did not join Orientation last week, this week is quite dreary. I know the people and I do run into them, but they are few and far between.
Anyway,

GEK1517 Mathematical Thinking
Lectures this semester are twice weekly, 1800 to 2000 hours. The lecturer and tutor is the idealistically-inclined Assoc. Prof. Leung. The beautiful poetry he weaves into Mathematics is only offset by his epic accent. The simple childlikeness of his lectures is only offset by the tutorial and past-year questions. I know now why they said this was a tough one, but it is so far very enjoyable.

Prof. Leung also conjectured that, in the film Inception, Dom Cobb fell from limbo into the next level, which is actually the real world itself. Dream layers and reality thus form a closed loop. A loopy proposition!

MA1505 Mathematics I
PC1431 Physics IE
Pre-allocated modules.
Maths I started very quickly, and covered functions as soon as briefing and the IVLE stuff are done with. Lecturer: Prof. Tan Ban Pin.

Physics IE had a bad start. Lecturer went on and on teaching what Physics is and why Physics is so important. Stuff like test timings, teaching cirriculum were pushed to the last few seconds. Lecturer: he didn't introduce himself.

CM1417 Fundamentals of Chemistry
I am taking this module as a punishment for being so stupid in J1 that I decided not to take H2 Chemistry.
I now have a different PC1431 lecture timing than the rest of my course, and also a different MA1505 tutorial slot because of this module. (Though how different it will turn out, I have yet to see.)

WP2201I Messing with Nature: Unintended Consequences
I am taking this module in lieu of EG1413 Critical Thinking and Writing, because it seems more interesting.

Actually I wanted WP2201G very much more. WP2201G concerns Language and Migration. Issues of language use and migration are to me what SNSD group member names are to many guys. So if I take it, life would be a breeze. Too bad it clashes with Maths, Physics and Chemistry all at once.

Lessons start tomorrow.

Close Shaves

Three unreasonably truncated travelogues in one entry, with a running theme.

December 2009: New Zealand - Fox Glacier
A path leads up to the glacier, ending in an observation post, a chain across our access and a sign saying No Tourists Without A Guide Beyond This Point. Half of my group, including Dad and Jamie, crossed this point without a guide in order to reach the glacier's head, which cannot be seen from the post. They disappeared behind the edge of a rock.

A few minutes later we heard a deep groan and crash as a piece of ice broke off from the glacier's head and crashed to the ground. I freaked out and ran towards the rock where they were last seen, expecting the worst, but found them all slightly surprised but unharmed.

If the stream flowing out from the glacier's head was any weaker, or more conveniently positioned, nothing would have stopped them from actually walking over and touching the ice, which would have put them in the way of the falling block. For an unappetising instant, I contemplated going home without two of the people in the family.

June 2010: China - Fuzhou
In the morning, we found my sisters' room in the hotel deserted... Their belongings were intact, but the door was wide open. I was especially paranoid about my sisters' safety for this trip; I took it to myself never to let them stray from my watch, all through the waking hours, but now I had to lose track of them at daybreak. For an unappetising instant, I contemplated going home without two of the people in the family.

We found them in the restaurant, having breakfast. It turned out to be a simple misunderstanding. Nevertheless I made sure they were sorry for what they had done. And what kind of bonehead leaves their bag in the room and the door open? Sheesh.

July 2010: Russia - Listvyanka
The day we landed in Irkutsk, Dad and I came to our hotel in Listvyanka on the shore, and had dinner in the cafe. There were boisterous Russians at the next table: a doctor and his wife from Irkutsk, and a lady from Angarsk (or was the lady from Irkutsk, and the couple from Angarsk?) who struck up a rapport with us. Soon a family from Moscow (a government worker, his wife, and their toddler daughter) came to join us and together they hauled us both onto the boat for a free one-hour cruise to nowhere, on fabled Lake Baikal.

We had never warmed up to strangers this quickly before. Less than thirty minutes into all the socialising (which featured a significant language barrier) we were rounded up and now we were partying together, far away from shore on that immense lake. Not having snapped out of China Mode entirely, I was shiteless inside. For an unappetising instant, I pictured Dad and myself, both knocked-out drunk, being thrown overboard into the freezing waters; Yea, the Doctor was very insistent in his spamming of tequila.

My fears were unfounded, evidently. My misty eyes drifted from one smiling face to the other. Not a chance would we splosh into the Baikal under their watch. They had families and came as families (except for the lady from Angarsk, who was alone then, but also had a family somewhere). And they were very nice. And we took a few more swigs of the drink, licks of salt, slices of lemon, and pledges of eternal friendship, and so on.

An hour later (or was it two?) we were ashore, many thanks be to God. There at the wharf we kissed the Russians goodbye. When we stumbled back to our room, we stumbled into the correct one, which proves that we were not too drunk, but we also fell asleep very quickly.